Un érudit pèse-t-il plus lourd qu’un ignare ?

De Boltzmann à Landauer

 

 On trouvera à l’adresse  http://maxdauchet.fr/ une version plus détaillée de cet article

Si la question du poids de la connaissance dans un cerveau fait sourire et n’a guère de sens, celle du poids de l’information chargée dans une clé USB est bien réelle et inspire les Youtubers.

On parle d’information dématérialisée quand elle est accessible sous forme numérique plutôt que stockée dans des bibliothèques soumises à des contraintes architecturales draconiennes tant le papier est lourd. Jusqu’où peut-on aller dans l’allégement du support ? Rien ou Presque rien ? « Rien » signifierait que l’information est immatérielle. « Presque rien » signifierait qu’elle a un lien irréductible avec la matière. Idéalisme d’un côté, matérialisme de l’autre ? éclairer le distinguo vaut le détour. Le chemin nous fait passer par la thermodynamique et l’entropie, celle-là même qui nous fascine quand il s’agit du cosmos, dont la formule S = k logW orne la sépulture de Boltzmann à Vienne. Il  aboutit à un « Presque rien » que quantifie le principe de Landauer.

Ce qu’en disent les Youtubers

Le Youtuber scientifique Théo Drieu a mis en ligne ce printemps la vidéo Combien pèse la totalité d’internet sur sa chaîne Balade Mentale (un million d’abonnés). Il ne s’agit bien entendu pas de la masse des infrastructures du net – des millions de tonnes – ni de l’équivalent en masse de l’énergie consommée – dans les 10 à 15 % de l’électricité de la planète. Il s’agit d’une estimation de la masse des électrons nécessairement mis en jeu pour faire circuler l’information sur le net. Dans la vidéo, l’animateur sacrifie à la loi du genre en tripotant une orange afin de marquer les esprits : la masse des informations sur le net serait celle d’une orange. Drieu ne fait là, comme il l’annonce, qu’actualiser les chiffres avancés par son collègue d’Outre-Atlantique Michael Stevens qui dans une vidéo de 2012 intitulée How Much Does The Internet Weigh? croquait modestement une fraise, les millions de térabits sur le net étant alors moins nombreux que maintenant. Dans cette même vidéo sur sa chaîne Vauce (vingt-deux millions d’abonnés) Stevens évoquait deux aspects : le nombre d’électrons nécessairement mobilisés selon les technologies du moment pour faire circuler l’information, et le nombre nécessaire pour la stocker. Dans ce cas, il estimait la masse inférieure à celle non plus d’une fraise mais d’une graine de fraise[i].

 Ce qu’en disent les chercheurs

Ce qu’en dit précisément la science est plus saisissant encore, car la limite théorique est des milliards de fois moindre que la masse d’une graine de fraise évoquée par Stevens. Pour le raconter mieux vaut le faire en énergie plutôt qu’en matière, puisque matière et énergie se valent selon la célébrissime formule d’Einstein E = m c².  Cela évite le biais lié à l’usage de la matière pour coder, que l’on peut ajouter, comme la plume encre le papier,  ou retrancher comme le burin incise la pierre.  D’autre part nous nous limitons ici au stockage, sans considérer la circulation de l’information.

La clé de voûte du raisonnement est le principe formulé en 1961 par Rolf Landauer, physicien américain chez IBM[ii] : l’effacement d’un bit dissipe au moins une énergie de k T log2 Joule, où k est la constante de Boltzmann, T la température absolue (en Kelvin) et log 2 ≈ 0,693. L’irruption de Boltzmann au milieu de l’informatique théorique peut surprendre, c’est pourtant lui qui fait le lien entre la physique-chimie – donc les sciences de la matière – et l’informatique – donc les sciences de l’information.

Landauer est pour sa part le premier à avoir tiré clairement toutes les conséquences de la théorie de Boltzmann. Les systèmes que considère Boltzmann sont des gaz, avec des milliards de milliards de milliards d’états possibles au niveau de l’ensemble des particules. Landauer applique l’idée de Bolzmann sur un système à … deux états, le 0 et le 1, juste de quoi stocker un bit. Pour étudier les propriétés d’un bit d’information, il applique ainsi un concept – l’entropie – basé sur quatre siècles d’intenses recherches en physique-chimie.  On comprend que les laboratoires de physique demeurent mobilisés pour monter des expériences de confirmation ou d’invalidation de la proposition de Landauer, car de leurs résultats dépend notre conception des rapports entre matière, énergie et information.  Ces expériences se situent au niveau quantique et font face à des phénomènes complexes comme les fluctuations statistiques d’énergie qui sont ici passés sous silence. Le présent regard est celui d’un informaticien, illustré par un petit démon imaginé par Maxwell, démon qui lui aussi a suscité de nombreuses vidéos.

L’entropie, une histoire de gaz et de piston

 Wikipédia définit l’entropie comme une grandeur physique qui caractérise le degré de désorganisation d’un système. Cette notion  naît de l’étude du rendement de la machine à vapeur et des travaux de Carnot sur les échanges de chaleur, autrement dit de la thermodynamique au sens littéral du terme. Le principe de Carnot dit que sans apport extérieur d’énergie, une source chaude et une source froide s’équilibrent irréversiblement en un système de température homogène. Ce principe a été généralisé en ce qui est maintenant le deuxième principe de thermodynamique, en introduisant la notion d’entropie pour quantifier « le désordre » vers lequel tout système sans apport extérieur d’énergie évolue inexorablement selon ce principe.

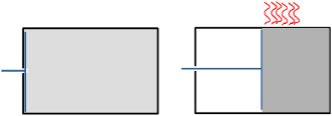Clausius relie en 1865 la baisse d’entropie d’un gaz parfait à la la chaleur que dégage le travail d’un piston qui comprime le gaz à température constante[iii].

 Quelques années plus tard, Bolzmann propose une définition radicalement différente de l’entropie S. Cette définition s’appuie sur la description statistique de l’état du gaz et aboutit à la formule  S = k log W déjà évoquée (la version étendue de cet article montre l’équivalence des deux approches).

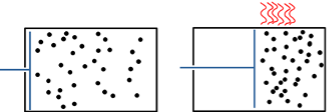W est la clé du lien avec le numérique, ce symbole  désigne le nombre de configurations possibles du gaz en considérant la position et de la vitesse de chaque particule. Quand le piston divise par deux le volume du gaz, le nombre possible de positions d’une particule est également divisé par deux :  Pour chaque particule, il n’y a plus à préciser si elle est à gauche ou à droite dans la boite. Landauer en déduira plus tard que c’est l’effacement de cette information pour chaque particule qui produit la chaleur.

Cette présentation de l’entropie de Boltzmann et de son interprétation par Landauer enjambe l’histoire. Entre temps, les réflexions des physiciens ont évolué pas à pas, et elles ne sont pas closes. Le démon de Maxwell illustre ces réflexions.

Le démon de Maxwell : quand le calcul et la mémoire s’en mêlent

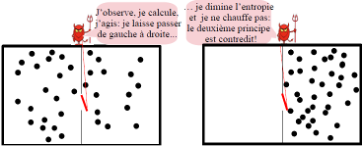Se plaçant comme Boltzmann au niveau des particules, Maxwell proposa une expérience de pensée comme les physiciens aiment à les imaginer.

Maxwell considéra une boîte partagée en deux par une cloison munie d’une trappe qu’un démon actionne sans frottement de façon à faire passer une à une des particules[iv]. En les faisant passer de gauche à droite, le démon « range les particules », il diminue l’entropie du gaz sans fournir de travail, contrairement au piston : le deuxième principe de thermodynamique est contredit !

Pour lever la contradiction, les physiciens cherchèrent du côté des calculs effectués par le démon de Maxwell, considérant que si celui-ci n’exerce pas sur le gaz un travail mécanique, il exerce en quelque sorte un travail intellectuel, il observe, il acquière de l’information et il calcule. Tel fut le point de vue de Szilárd, un des principaux scientifiques du projet Manhattan connu pour son opposition farouche à l’usage de la bombe atomique[v]. Puis Brillouin[vi] ébaucha l’idée ensuite érigée en principe par Landauer que c’est l’effacement d’information qui augmente l’entropie, comme nous allons le préciser.

Le principe de Landauer : du gaz à l’ordinateur

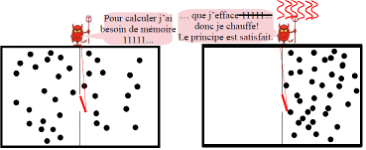Le principe de Landauer est une extrapolation de la formule de Boltzmann aux systèmes informatiques. La relation entre énergie et nombre de micro-états est étendue par analogie.

Landauer pose directement la formule de Boltzmann  en considérant un seul bit de mémoire comme un système à deux états possibles, 0 et 1 [vii]. Si le bit est effacé, il n’y a plus qu’un seul état, l’entropie a donc diminué et ce travail d’effacement s’est dissipé en chaleur. 

Retour sur le démon de Maxwell 

Pour la simplicité de l’interprétation numérique, nous avons seulement considéré plus haut le cas où le volume du gaz est réduit de moitié. Mais le parallèle entre le piston et le démon doit tenir pour tous les taux de compression. Pour pouvoir revenir aux conditions initiales, le démon doit compter les particules de gauche à droite, afin d’en renvoyer autant si l’on poursuit le parallèle avec le piston. D’après Landauer, pour ne pas chauffer, le démon ne doit effacer aucun bit intermédiaire, ce qui n’est pas le cas avec l’addition habituelle mais est réalisé par exemple en « comptant des bâtons ». Or le démon fait partie du système physique considéré dans l’expérience de pensée, il doit donc être remis dans son état d’origine si l’on veut faire un bilan énergétique à l’issue de la compression comme c’est le cas ici. Autrement dit, il doit alors effacer sa mémoire, ce qui dégage la chaleur prévue par la physique. 

Réversibilité et entropie

Pour imaginer un système informatique ne consommant aucune énergie, ce système ne doit donc effacer aucune information durant ses calculs, ce qui revient à considérer des machines logiquement réversibles, où l’on peut remonter pas-à-pas les calculs comme si on remontait le temps . C’est ainsi que nous avons réinterprété le démon. Les opérateurs logiques et arithmétiques usuels ne sont évidemment pas réversibles (l’addition et le ET perdent les valeurs de leurs données) . Cependant Bennett[viii]^{, [ix], [x]} a montré que l’on peut rendre tout calcul logiquement réversible en donnant un modèle de machine de Turing conservant l’historique de tous ses calculs. Ces considérations sont particulièrement prometteuses pour les ordinateurs quantiques, où la superposition d’états dans les q-bits conduit (sous les nombreuses contraintes liées à ce type de machine) à considérer directement des opérateurs réversibles.

Les physiciens continuent de se passionner pour le principe de Landauer[xi], imaginant des nano machines parfois extravagantes, à cliquets, escaliers, poulies ou trappes et construisant des expériences de plus en plus fines[xii] pour mesurer l’énergie dégagée par l’effacement d’un bit[xiii]. Jusqu’à présent, le principe est confirmé, dans le cadre de la physique classique comme de la physique quantique. Il n’est cependant pas exclu que sa limite soit un jour abaissée, notamment en exploitant des propriétés de la physique quantique encore mal connues. Cela remettrait en cause les interprétations qui viennent d’être décrites, et ce serait alors une nouvelle source de progrès dans les modèles scientifiques de l’organisation de la matière et de l’information.

En guise de conclusion

La limite de Landauer commence à influencer l’architecture des systèmes et plaide pour l’informatique quantique. Elle fournit un horizon qui nous incite à méditer sur ce qu’est le traitement de l’information, que ce soit par le vivant ou la machine.

La théorie associe à l’information une masse minimale de matière  bien moindre encore que celle mise en scène par les Youtubers, déjà spectaculaire par sa modicité.  De même il faut peu de matière pour libérer beaucoup d’énergie (bombe, centrale nucléaire) et beaucoup d’énergie pour générer quelques particules (au LHC du CERN). Le second principe de thermodynamique et l’entropie nous font penser qu’il est plus facile de désordonner que de structurer. Pourtant l’univers fabrique sans cesse de nouveaux objets cosmiques et la vie s’est développée sur terre[xiv]. Nous devons nous méfier de nos appréciations sur le petit ou le grand, le beaucoup ou le peu, qui sont des jugements attachés à notre échelle et à notre condition.

Max Dauchet, Professeur Émérite de l’Université de Lille.

[i] Estimation tirée d’articles universitaires. Cinquante ans avant, Richard Feynman, prix Nobel de physique , dans sa célèbre conférence de 1959 intitulée There’s Plenty of Room at the Bottom, annonciatrice de l’essor des nanotechnologies, estimait que l’on pourrait coder avec les technologies de l’époque toutes les connaissances du monde dans un grain de poussière, et indiquait les pistes pour le faire.

[ii] Rolf Landauer, Irreversibility and Heat Generation in the Computing Process, IBM Journal of Research and Development, 5(3), 183–191 (1961).

[iii] Die mechanische Wärmetheorie, Friedrich Vieweg und Sohn ed (1865 -1867).

[iv] Historiquement, le démon trie les particules les plus rapides et les plus lentes, distribuées statistiquement autour de la valeur moyenne, pour créer une source chaude et une source froide  à partir d’un milieu en équilibre thermique.

[v] La première planche de La bombe, BD consacrée au projet Manhattan, illustre un cours de Szilárd sur le sujet en 1933. Alcante, Bollée, Rodier, Ed. Glénat, 2020.

[vi] Brillouin est sans doute un des noms les moins connus de ceux cités ici. Alfred Kastler, prix Nobel de physique, lui rendait hommage dans les colonnes du Monde lors de sa disparition 1969 : Léon Brillouin : un des plus brillants physiciens français.

[vii] En réalité un réseau de bits statistiquement liés, pour des raisons de phénomènes physiques.

[viii] C. H. Bennett, Logical reversibility of computation, IBM journal of Research and Development, 1973.

[ix] J.-P. Delahaye, Vers du calcul sans coût énergétique, Pour la science, pp 78-83, janvier 2017

[x] C. H. Bennett, Notes on Landauer’s Principle, Reversible Computation, and Maxwell’s Demon, 2002       https://arxiv.org/abs/physics/0210005

[xi] La plupart des références données ici sont les références historiques – il est souvent instructif de découvrir les idées « dans leur jus ». Cependant il suffit de parcourir le net pour en trouver des récentes en pagaille.

[xii] Les fluctuations statistiques ici négligées y jouent un rôle important.

[xiii] Séminaire information en physique quantique  de l’Institut Henri Poincaré, 17/11/2018 . vidéos sur carmin.tv, les mathématiques vivantes. Landauer et le démon de Maxwell, Sergio Ciliberto. Thermodynamique et information, Kirone Mallik.

[xiv] Dans son article déjà cité, Bennett évoque l’économie de moyens de la duplication des gènes, déjà remarquée  par Landauer en 1961.