Sur Interstices, la revue scientifique sur les sciences du numérique, Maurice Nivat, ce père de l’informatique théorique qui vient de nous quitter, partageait il y a presque dix ans son émerveillement pour la révolution conceptuelle à laquelle il a grandement participé. Un grand merci de nous permettre de reprendre ce billet ici. Thierry Viéville.

En 1970, Maurice Nivat, jeune mathématicien, et Marcel-Paul Schützenberger, son père spirituel, nommé depuis peu au directoire de l’IRIA (ancêtre de l’INRIA) avec Henri Boucher, André Lichnerowicz et Jacques-Louis Lions, préparent un événement pour le moins inédit : une conférence de presse pour annoncer la naissance officielle de ce qu’ils baptisent « l’informatique théorique » ! « Je ne sais pas ce qui nous a pris ce jour-là, reconnaît Maurice Nivat. Toujours est-il que près de 40 ans plus tard, la discipline existe bel et bien et que le nombre de chercheurs concerné a été multiplié par cinquante si ce n’est cent. »
De même, les trois grands chapitres qu’ils énoncent à l’époque, devant une quinzaine de journalistes spécialisés, ont perduré : la théorie des automates et des langages, l’algorithmique et, la théorie de la programmation. Maurice Nivat rappelle ce passé avec une pointe d’étonnement et d’amusement rétrospectif : « On ne s’est finalement pas trompés ». Il faut dire qu’ils n’étaient pas tout à fait novices : leur passion commune pour cette discipline émergente n’était pas nouvelle : « Il nous a fallu environ dix ans, entre 1960 et 1970, pour comprendre ce qu’étaient les langages de programmation, apprendre à les compiler, les traduire, rappelle Maurice Nivat. Cela peut paraître long mais il faut se replacer dans le contexte de l’époque, des machines à calculer programmées en langage machine – on ne parlait pas encore d’ordinateurs mais de machines (ou « bécanes »), ni d’informatique mais de calcul automatique – , des cartes perforées, où toute erreur de poinçonnage se payait au prix de la vérification de la totalité des cartes. »
Pionnier de la théorie des automates
C’est à l’Institut Blaise Pascal (le centre de calcul du CNRS qui avait très récemment acquis son premier ordinateur pour remplacer les anciennes machines à manivelle) que dirigeait alors René De Possel, que Maurice Nivat découvre l’informatique, en 1959, à un moment où la discipline n’existait pas encore (le mot apparaît vers le milieu des années 1960). Les chercheurs tentent alors de commander, de « programmer » la toute nouvelle machine de l’Institut : une Bull Gamma AET, une incroyable machine, parmi les premières en France, installée dans la cave, « qui devient rapidement notre temple de la mathématique ». Normalien, théoricien dans l’âme, Maurice Nivat est d’emblée attiré par les langages de programmation de ces machines à calculer, des langages « auxquels pas grand monde ne comprenait grand chose ». On en compte trois en gestation à l’époque : Fortran (le langage des machines d’IBM), Algol 60 développé par un groupe international et Lisp, le langage conçu par John McCarthy.
« Une seule personne était vraiment capable de faire marcher cette machine : Louis Nolin ! », aime t-il à rappeler, évoquant ainsi son autre maître à penser. Logicien autodidacte, Louis Nolin a commencé par une formation en philosophie avant de s’intéresser à l’informatique. Il a très tôt imaginé qu’on pouvait raisonner sur les programmes comme sur n’importe quel objet mathématique, qu’il devait y avoir une théorie à construire, sur des bases mathématiques, pour faire faire des calculs à ces machines.
Pourtant, rappelle t-il, « le décalage entre les espoirs que faisait naître l’informatique et les possibilités de ces machines était énorme. On pensait pouvoir tout calculer… mais il fallait pas moins d’une seconde pour aller chercher une seule information sur le tambour de la machine, qui comptait 64 registres en tout et pour tout ! C’était tout simplement un exploit d’inverser une matrice de 15 par 15, un problème mathématique relativement simple que l’on résout aujourd’hui par ordinateur sur des matrices de 450 000 x 450 000 ! ». Ainsi, avec Louis Nolin, il lui a fallu presque deux ans pour concevoir un compilateur d’environ 3 000 lignes de code.
Une révolution conceptuelle
 |
| Marcel-Paul Schützenberger lors du colloque ICALP en 1972. © INRIA |
Maurice Nivat rencontre Marcel-Paul Schützenberger, « Schütz » comme il dit, en 1963 : une révélation. Ce mathématicien autodidacte, psychiatre et médecin de formation, « s’était mis aux mathématiques pendant une de ses campagnes de vaccination pour l’OMS (Organisation mondiale de la santé) en Indonésie… parce qu’il s’ennuyait ». Libertaire, anarchiste, élitiste, maniant avec plaisir le paradoxe, intéressé par tous les problèmes scientifiques, curieux de tout, c’était aussi une des figures de Saint-Germain des Prés aux côtés de Juliette Greco et Boris Vian, qui l’a décrit sous les traits de « l’abominable Docteur Schütz » dans un de ses livres. C’était surtout un génie mathématique.
Sous sa direction, il prépare sa thèse d’Etat en mathématiques, présentée en 1967, sur « les transductions des langages de Chomsky », des objets mathématiques entièrement développés par des informaticiens. Une première ! « À l’époque, considérer l’informatique comme une discipline mathématique était une véritable révolution conceptuelle, ajoute t-il. La Faculté des sciences de Paris ne comptait pas plus de 15 à 20 professeurs de mathématiques, c’était un cercle fermé, très élitiste et Schütz était très tendu quand j’ai présenté ma thèse, quelque peu exotique mais finalement bien acceptée. »
Il se souvient « d’une période miraculeuse : on rencontrait des gens de toute espèce. Toutes les opinions étaient bonnes, équiprobables, c’était une période passionnante où tout était à faire, notre champ d’action était pratiquement illimité. Pas besoin de réflexion prospective. » Pendant ces années de gestation de l’informatique, Maurice Nivat met aussi sur pied les premiers programmes d’enseignement de l’informatique dans des universités françaises, à Grenoble et Rennes où il est chargé de conférences pendant sa thèse : « on écrivait les programmes de licence sur un coin de table, dans un bar ! Il m’arrivait d’enseigner le mercredi ce que j’avais appris le mardi soir ! »
Des langages dotés d’une sémantique
Cet enthousiasme est encore accru lorsqu’en septembre 1969, il découvre la « théorie de la programmation », en participant à une réunion à Colchester (Grande-Bretagne) qui réunit les fondateurs de la discipline, Dana Scott, Robin Milner, Christopher Strachey, Peter Landin, David Park… Il découvre que les programmes eux-mêmes, ces objets étranges sans véritable statut, peuvent être considérés comme des objets mathématiques, susceptibles de théorèmes. Ces théories prendront beaucoup d’importance par la suite pour la vérification de programmes, pour la production et la manipulation de logiciels de plus en plus gros et complexes.
Convaincu de l’importance de cette voie de recherche, il n’hésite pas, quelques mois plus tard, en 1970, à placer la théorie de la programmation comme un des trois chapitres fondamentaux de l’informatique théorique, aux côtés de la théorie des automates et des langages sur lesquels il travaille depuis dix ans et l’algorithmique, qui s’est finalement assez peu développé en France bien que les problèmes qu’elle soulève soient innombrables, comme les problèmes dits NP-durs. Aujourd’hui encore, ce professeur émérite à l’Université Denis-Diderot (Paris VII) milite pour sensibiliser les théoriciens aux applications et réciproquement : un débat qui battait son plein dans « ce fabuleux lieu de création qu’était le bâtiment 8 » partagé avec Gérard Berry, Gérard Huet, Philippe Flajolet, Gilles Kahn, Jean Vuillemin, Jean-Marie Cadiou, Jean-Jacques Lévy, Bruno Courcelle, entre l’école française très théoricienne des langages formels, parfois sectaire autour de Schützenberger et des chercheurs inspirés du modèle américain de la programmation.
 |
| Maurice Nivat lors du colloque ICALP, ici avec Maurice Gross. © INRIA |
L’émulation s’étend à l’échelle européenne quand, avec Marcel-Paul Schützenberger, ils créent l’Association européenne d’informatique théorique (EATCS European Association for Theoretical Computer Science), dont le premier colloque baptisé ICALP (International Colloquium on Automata, Languages and Programming) a lieu en 1972 à l’IRIA. Les grands noms de la discipline sont au rendez-vous : Michael Rabin, Michael Paterson, Dana Scott, Albert Meyer, Samuel Eilenberg, Corrado Boehm. L’EATCS compte aujourd’hui 2 000 personnes. En 1975, Maurice Nivat lance aussi une revue scientifique, qui fait toujours référence : TCS (Theoretical Computer Science), dont il est rédacteur en chef pendant 25 ans. La revue a publié pas moins de 100 000 pages en 25 ans.
Le regard du chercheur sur l’informatique
Loin de rester cantonné dans le bâtiment 8 et son monde aussi ouvert soit-il de chercheurs et d’étudiants en langages algébriques, en sémantique, en parallélisme, Maurice Nivat accepte en 1982 la lourde tache de réfléchir pour les ministères de l’éducation nationale et de la recherche, à la filière électronique. À la suite de son rapport (Savoir et savoir-faire en informatique), il lance une dizaine de « programmes de recherche coordonnés » financés par le programme mobilisateur de la filière électronique qui réunit chercheurs et industriels, dont il préside le conseil scientifique de 1982 à 1992. Intelligence artificielle, architecture machine, parallélisme, programmation… sont autant de sujets qui ont pu bénéficier de ces fonds : « cela a joué un grand rôle dans la recherche en informatique en France » reconnaît-il.
Pourtant son regard sur l’état actuel de la science informatique est amer : « On nous commente avec emphase les succès d’Ariane ou du TGV… mais les princes qui nous gouvernent ont abandonné l’informatique, pourtant clé de ces succès. Je ne comprends toujours pas pourquoi. Aux États-Unis, l’informatique est l’enjeu du moment, le bouillonnement d’idées y est relayé, financé par les agences fédérales, par les banques… Cette émulation n’existe pas en France : le logiciel n’est pas pris au sérieux, les financements ne sont pas octroyés au bon moment, on finance la création de start-up prometteuses mais ensuite, on ne leur donne pas les moyens de leur développement. » « Les chercheurs en informatique font les frais de l’absence de champ d’application de leurs recherches en France et en Europe, toutes deux dénuées d’industrie informatique, ajoute t-il. C’était criant, en octobre 2007, lors de la première demi-journée consacrée à l’informatique à l’Académie des sciences : nous y avons entendu des exposés brillants mais tellement éloignés de l’informatique réelle, de ce que font les machines. » Selon lui, une révolution totale est nécessaire. La priorité est de décider l’éducation nationale à prévoir un enseignement informatique dans les collèges et les lycées, que l’informatique soit enfin considérée, en France, comme une discipline à part entière. Construire l’avenir suppose de former les jeunes. C’est seulement à ce prix que l’informatique fondamentale restera inventive, ouverte sur les autres disciplines, que ce soit la biologie, la linguistique… et toutes sortes d’applications.
Contrepoint
Maurice Nivat a contribué à la formation de nombreux acteurs de la recherche en informatique. L’un d’entre eux, Max Dauchet, Directeur du centre de recherche INRIA Lille – Nord Europe, nous apporte son témoignage :
« Maurice Nivat a été mon maître, comme il l’a été pour nombre d’entre nous, tant par sa science que par sa personnalité. Et il demeure mon maître. Ses intuitions sont toujours vivantes dans mon esprit – ses indignations aussi. Dans un monde informatique naissant et hésitant, il fut pour nous un repère, tant sur le plan de la science que de son rôle dans la société. Et il le demeure. Comme beaucoup de précurseurs, Maurice n’a jamais été vraiment à la mode. Avoir raison trop tôt est un combat difficile, d’où un certain pessimisme – qui n’a jamais altéré sa combativité. De ce fait, Maurice sous-estime l’influence déterminante qu’il a eue sur la recherche française et européenne en informatique. Ceci mériterait un travail d’érudition. Si l’on mettait bout à bout le devenir de tous ceux et celles qu’il a formés et marqués à vie, l’impact de ses initiatives (EATC, TCS, ICALP, les PRC…), on mesurerait sans doute mieux tout ce que la société lui doit. Merci Maurice. »
Bellin Version originale : https://interstices.info/maurice-nivat-une-vision-a-long-terme-de-la-recherche-en-informatique, publié le 17/03/2008




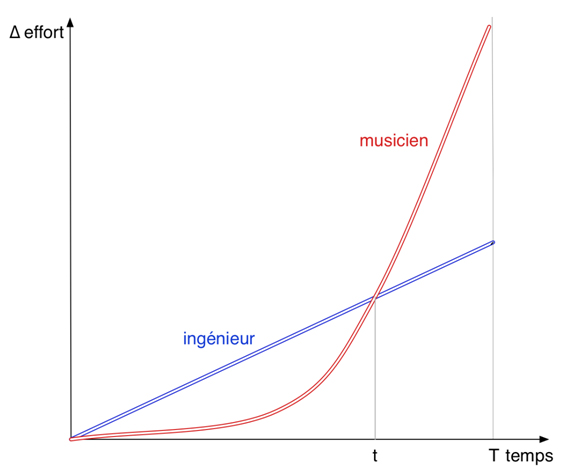








 Nous retrouvons aujourd’hui,
Nous retrouvons aujourd’hui, 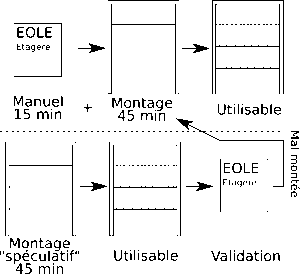





















![By Tibidibtibo (Own work) [CC BY-SA 3.0 (http://creativecommons.org/licenses/by-sa/3.0)], via Wikimedia Commons](/wp-content/uploads/2015/11/Plan_metro_tram_chemin.svg_-300x223.png)