Quel est le point commun entre les battements de mon cœur, un avion qui vole grâce à ses réacteurs et l’évacuation d’une salle de cinéma ? C’est ce que vont nous expliquer Jean-Antoine Désidéri et Alain Dervieux (Inria, Sophia Antipolis Méditerranée) en nous accompagnant à travers un demi-siècle de calcul scientifique, du point de vue de l’étude des fluides. Pascal Guitton et Thierry Viéville.
Bonjour, vous êtes des spécialistes de calcul scientifique et de mécanique des fluides numériques. Pourriez-vous nous préciser le contour de ces disciplines ?
On peut dire que tous les scientifiques s’impliquent dans une forme de “calcul sur ordinateur”, mais classiquement on emploie le terme de calcul scientifique (et celui de numéricien·ne pour celles et ceux qui le pratiquent) pour désigner les activités de modélisation physique, mathématique et informatique de systèmes complexes issus de la physique théorique ou de l’ingénierie.
Les équations qui régissent l’évolution temporelle de ces systèmes sont dites « équations différentielles » et celles qui tiennent compte aussi des aspects spatiaux sont dites « équations aux dérivées partielles« . Calculer des solutions approchées de ces équations aux dérivées partielles est l’objet de la simulation numérique. Le problème doit être réduit à un nombre raisonnable d’inconnues. Pour cela, on construit un maillage en décomposant l’espace en un assez grand nombre de petits éléments géométriques. Chaque élément porte les valeurs locales des inconnues. L’art du numéricien consiste à établir des relations entre ces inconnues de manière à approcher finement l’équation aux dérivées partielles.
Lorsque ces méthodes sont appliquées à la simulation d’écoulements de fluides (liquides, gaz, plasmas), on parle de mécanique des fluides numérique.
Vous avez rejoint l’INRIA au début des années 80. Quelle y était alors la situation du calcul scientifique ?
En mathématiques appliquées, la culture scientifique était celle des Éléments Finis (EF) et de la Théorie du Contrôle. Sur ces sujets, l’INRIA entretenait un lien très étroit avec l’Université Pierre et Marie Curie (Paris 6) et l’École Polytechnique notamment grâce à l’implication des Professeurs P.G. Ciarlet, R. Glowinski, J.L. Lions et P.A. Raviart. Ce lien est toujours vivace, mais bien d’autres ont été créés depuis, comme en témoigne la diversité thématique d’Inria aujourd’hui.
Nous allons nous concentrer sur les thématiques de la simulation et aborderons peu ici les thématiques du contrôle qui sont pourtant très importantes, notamment pour leurs applications à la robotique.
Dans cet environnement, en matière de simulation, le calcul scientifique côté INRIA était porté par trois équipes-projets. L’une développait une bibliothèque de calcul par éléments finis très généraliste, bien que fortement orientée vers la problématique de la mécanique du solide, typiquement le calcul des structures (utilisés par exemple pour construire un pont, un avion…). L’autre développait des méthodes par éléments finis pour la simulation des ondes et les problèmes inverses, notamment en recherche pétrolière. La troisième se focalisait sur la méthodologie numérique, et comportait un volet particulier en mécanique des fluides. Nous sommes des héritiers plus particulièrement de cette équipe, alors dirigée par R. Glowinski qui est associé aujourd’hui à l’Université de Houston.
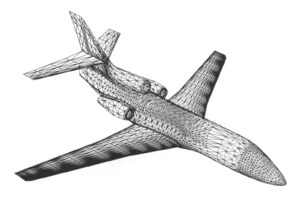
En mécanique des fluides, le développement numérique portait sur les équations de la vitesse de ce fluide. Une réalisation particulièrement marquante a été le calcul d’un écoulement aérodynamique tridimensionnel autour d’un avion complet sur un maillage de quelques milliers de points, en collaboration avec Dassault-Aviation:
 |
 |
| Écoulement potentiel autour d’un avion complet en maillage non structuré [1]. Cliquer pour zoomer. |
En calcul scientifique, une estimation des capacités d’un code est fournie par le nombre de points de maillage qu’il permet de traiter en une nuit avec le plus puissant ordinateur disponible. Début 80, grâce au calcul vectoriel (ordinateur Cray), les “gros calculs” sont passés de quelques dizaines de milliers de points à plusieurs millions.
Quelle était la motivation à poursuivre des recherches en mécanique des fluides numérique et quels étaient les sujets difficiles de l’époque?
En mécanique des fluides, la méthodologie dominante (notamment utilisée à la NASA ou à l’ONERA en France) était issue de techniques classiques d’approximation des équations continues par des calculs pas à pas, dit aux différences finies (DF). Ces schémas d’approximation sont simples à construire, et se généralisent aisément. Pour des objets courbes, il faut construire au préalable d’un maillage régulier, qui est ensuite déformé.
On parle de maillage régulier ou structuré quand les sommets des facettes sont organisés de façon structurée (par exemple avec uniquement des parallélépipèdes) et qu’il est donc possible de les stocker et de les traiter avec une matrice. Une règle de construction simple permet alors d’obtenir les positions des sommets et l’organisation des facettes.
Dans le cas contraire, le maillage a une forme libre, ce qui est plus souple mais plus lourd à manipuler.
Cette approche se justifiait tant qu’on abordait des problèmes de mécanique des fluides pour des géométries relativement simples. Mais avec l’ambition impérieuse de l’industrie aéronautique de traiter le “problème mythique » de l’avion complet, c’est-à-dire de résoudre les équations de la mécanique des fluides dans le domaine tridimensionnel défini par l’extérieur de la véritable géométrie d’un avion (sa forme), il fallait adopter une autre démarche. Le défi technologique a été de générer d’un maillage non structuré, plus souple, avec moins d’éléments tout en conservant la même précision. Par contre, cette perte de structuration dans le maillage entraine d’avoir à stocker dans l’ordinateur un grand volume d’informations pour connecter des points avec leurs voisins. Au tout début, ce stockage était en butée avec les limites de mémoire des ordinateurs dont nous disposions. Mais la communauté française des mathématiques appliquées avait aussi changé de méthode de calcul: la méthode des éléments finis que nous citions se rattache aux maillages non structurés. Ce travail sur les méthodes numériques en maillages non structurés fut pionnier.
Simultanément, la communauté internationale cherchait à développer des schémas d’approximation plus sophistiqués pour ces problèmes afin de traiter de manière plus savante les cas où les solutions attachées à ces problèmes devenaient singulières: lors de chocs. Un choc est une discontinuité dans la solution. Par exemple, lorsqu’un avion franchit le « mur du son’’, il crée un saut de pression qui peut gravement endommager le tympan. En régime de croisière d’un avion de transport moderne présente un saut de la pression de l’air, un choc sur la voilure, à la limite. L’optimisation aérodynamique consiste pour une grande part à réduire l’intensité de ce choc. Mais avant d’optimiser, il faut développer la capacité de simuler l’écoulement avec précision, donc à capturer les chocs.
En cette matière, un schéma dit conservatif permet de calculer avec précision les sauts des grandeurs physiques au travers d’un choc. Cependant, généralement, la solution numérique présente aussi localement des oscillations parasites qu’il convient de maitriser au mieux. Ces questions sont centrales en matière d’équations aux dérivées partielles pour la mécanique des fluides.
Certains de nos collègues comme Harten et van Leer ont proposé des solutions numériques qui présentent moins d’oscillations parasites. Un défi pour nous était alors de construire de tels schémas dans notre contexte avec les éléments finis et les maillages non structurés. Un autre défi – toujours d’actualité – était de développer des techniques de résolution les plus économiques possibles en mémoire et temps calcul, afin d’aborder efficacement des problèmes de grande taille. Nos efforts ont porté sur la stabilité des schémas de calcul numériques. Nous sommes heureux d’avoir pu contribuer à étendre ces méthodes et de les partager très largement en enseignant à travers l’Europe, comme à l’Institut Von Karman de mécanique des fluides de Bruxelles.
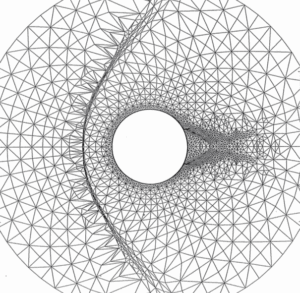
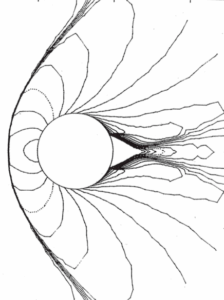
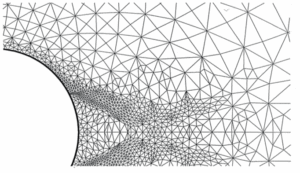
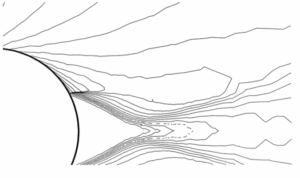
Écoulement supersonique autour d’un cylindre; approximation de type volumes finis en maillage non structuré adapté à l’écoulement [2]. A gauche le maillage utilisé vu d’ensemble (en haut) et détaillée (en bas). À droite on représente le flot du fluide. Cliquer pour zoomer.
Pour illustrer cela, observons grâce à la figure un cas-test dans lequel les équations d’Euler (fluide compressible) ont été résolues en deux dimensions d’espace dans le domaine extérieur à un cylindre. Ces résultats sont tirés d’un atelier international tenu à Rocquencourt en 1985. C’est un écoulement supersonique, à Mach 3, autour d’un cylindre, de gauche à droite. On voit devant le cylindre une ligne de choc au niveau du flot et on voit à gauche que le maillage s’est adapté au mieux au phénomène observé. Derrière le cylindre, la zone triangulaire est de vitesse nulle (on parle d’eau morte), et dans le sillage du cylindre l’écoulement s’accompagne d’autres phénomènes complexes.
Nos techniques d’approximation en maillage non structuré avaient alors permis, grâce à l’adaptation de maillage par déplacement des nœuds et division des éléments, de mettre en évidence de telles structures physiques avec précision.
Vous avez donc atteint dans les années 80 une certaine maîtrise des schémas d’approximation de type volumes-finis en maillages non-structurés. Quelles ont été les évolutions dans la décennie suivante?
La décennie 90 a été marquée par l’extension des méthodes de simulation à des cas de physique des fluides plus complexes, notamment motivés par certains programmes spatiaux européens. Le programme de fusée Ariane a soutenu une activité de recherche dans le domaine de la combustion. Dans certains laboratoires du CNRS, la recherche a porté sur la modélisation physique des phénomènes. À l’INRIA et dans d’autres laboratoires, les méthodes d’approximation ont été étendues pour traiter la cinétique chimique liée à la combustion, et le suivi de solutions instationnaires (propagation de flammes).
Le projet européen de navette spatiale Hermès a été un formidable moteur pour la recherche et le développement en matière de modélisation physique, d’expérimentation en soufflerie, de modélisation mathématique et de simulation numérique. Il a regroupé une soixantaine de laboratoires travaillant en émulation sur un ensemble de problématiques liées aux défis que soulève la validation du calcul des caractéristiques de vol de rentrée atmosphérique de l’engin. Sans être exhaustif, ni trop détaillé, notons au moins deux types de phénomènes physiques qui ont motivé l’extension des méthodes standards de simulation numérique en mécanique des fluides
- l’atmosphère raréfiée à très haute altitude, disons 80 km;
- les gaz hors équilibre thermodynamique, avec un point critique à 75 km d’altitude.
En atmosphère raréfiée, les modèles de mécanique des fluides sont de nature statistique. Cette situation a justifié le développement d’outils de simulation d’évolution d’un gaz hors équilibre (équations de Boltzmann), notamment en utilisant des méthodes aléatoires (simulation par la méthode de Monte-Carlo), ou ne pouvant décrire exhaustivement les éléments, on les sélectionne au hasard et de manière pertinente.
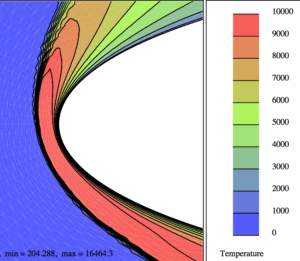
En pénétrant les premières couches de l’atmosphère lors de la phase de rentrée, l’engin est encore à très grande vitesse (25 fois la vitesse du son, soit 7 km/s). L’intensité du choc en amont du nez arrondi est alors suffisante pour dissocier les molécules d’air et le fluide est le siège d’un phénomène chimique qui absorbe en partie seulement le choc thermique. Pour cette raison, la paroi de l’engin est revêtue de dispositifs de protection spéciaux, dont les fameuses tuiles de la navette spatiale américaine. Plus généralement, le fluide, dans la couche de choc, subit différentes formes de déséquilibre thermodynamique. Dans l’enveloppe de vol de la navette, le point le plus critique vis-à-vis du choc thermique survient à 75 km d’altitude. Dans la simulation, on doit alors compléter les équations de la mécanique des fluides (équations de Navier-Stokes) par d’autres équations aux dérivées partielles dont chacune modélise une variable physique en déséquilibre, et tenir compte de manière complexe du mélange gazeux. Pour “valider” les calculs qui en résultent, il faut confronter les codes numériques entre eux, c’est la “vérification”, et les résultats de codes à ceux d’expériences en soufflerie. Cette validation est particulièrement difficile car en laboratoire, on ne peut reproduire la totalité des conditions du vol réel, et on procède par vérifications croisées de vérification et validation. Pour illustrer cette problématique, on montre ci-dessous un calcul de température autour d’une géométrie de double-ellipse utilisée pour représenter la partie avant de la navette.
 |
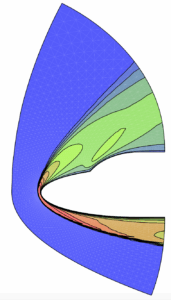 |
| Écoulement hors-équilibre chimique du mélange gazeux autour d’une double-ellipse; à droite un zoom du champ de température [3]. Cliquer pour zoomer. |
Outre les simulations de physique des fluides complexes, on a vu apparaître des simulations couplant plusieurs physiques, chacune associée à un modèle relativement classique. Notons en particulier les simulations de couplage fluide-structure dont voici une illustration :
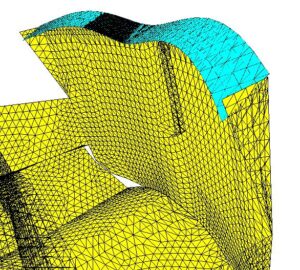 |
| Maillage tridimensionnel d’environ 100,000 points utilisé pour le calcul couplé fluide-structure d’un écoulement dans un inverseur de poussée du réacteur d’un avion de ligne. L’axe du réacteur de forme cylindrique se distingue en bas. L’écoulement va de gauche à droite. À droite, son chemin est barré par la cloison verticale. Il est à nouveau dévié vers la gauche par le volet élastique bleu dont on observe la forte déformation. Le but de l’étude était d’analyser la vibration parasite de ce volet. (R. Lardat, B. Koobus, E. Schall, A. Dervieux C. Farhat: Analysis of a possible coupling in a thrust inverter, Revue Européenne des Eléments Finis, 9:6-7,2000). Cliquer pour zoomer. |
De votre point de vue quelles ont été les principales avancées méthodologiques de votre domaine apparues dans les années 2000?
Les grands programmes spatiaux précédemment cités étaient nés de la volonté des autorités de maintenir la communauté scientifique européenne à un niveau scientifique et technologique compétitif au plan international. Au tournant du siècle cette volonté est devenue moins impérative, et les soutiens à la recherche appliquée ont davantage été trouvés dans le cadre des projets et réseaux de la commission européenne, notamment en aéronautique civile, à nouveau.
Les innovations méthodologiques les plus marquantes concernent les schémas d’approximation des calculs et les problématiques d’optimisation pour trouver les meilleures solutions approchées.
Mais c’est aussi l’ouverture de ces méthodes vers des applications hors du champ de la Défense Nationale : notamment en biologie, par exemple dans une action collaborative entre plusieurs équipes sur la modélisation de l’activité cardiaque (CardioSense). Voici une illustration de la simulation de l’onde électrique dans le cœur.
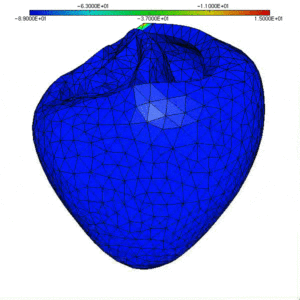 |
| Onde électrique dans le cœur, premiers travaux dans le cadre du projet Icema : on modélise la diffusion entre deux domaines avec leur potentiel électrique, en tenant compte de la structure membranaire permettant les échanges ioniques (Y. Coudière, 2000). Cliquer pour animer. |
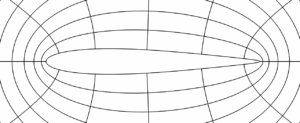
Voici maintenant la représentation d’un écoulement visqueux autour d’un profil très effilé. Ce calcul (récent) allie une méthode ancienne dite d’approximation de Galerkin discontinue combinée à une technique de représentation par des petites portions de courbes.
 |
 |
 |
| Écoulement autour d’un profil d’aile par la résolution des équations de la mécanique des des fluides (R. Duvigneau, 2017). Cliquer pour zoomer. |
Ces progrès réalisés, quelles sont les tendances actuelles dans vos domaines de recherche ?
Tout d’abord, on observe une prise en compte de plus en plus systématique des incertitudes et de l’utilisation du hasard dans plusieurs types d’approche, pour résoudre les équations avec des approximations qui utilisent des tirages aléatoires.
Par ailleurs, on note également le haut degré de sophistication atteint aujourd’hui par les générateurs de maillages, et les logiciels d’adaptation. On note aussi dans ce domaine des progrès notoires dans l’étude de phénomènes avec des ruptures ou des changements rapides. Pour illustrer ce dernier point voici une animation montrant l’évolution d’un maillage tridimensionnel modélisant une zone urbaine dans laquelle se produit une détonation.
 |
| Maillage évolutif suivant une onde de détonation en milieu urbain (F. Alauzet, 2017). Cliquer pour animer. |
Voici maintenant une illustration des progrès réalisés en matière d’approximation, y compris dans ces cas instationnaires, et du volume de calcul que l’on peut traiter sur nos architectures. Il s’agit d’un problème classique de résolution d’instabilité atmosphérique (dit de Kelvin-Helmholtz). Les équations de la mécanique des fluides sont résolues avec 4 millions de degrés de liberté sur une architecture machine à 256 cœurs. Le schéma d’approximation dont on a besoin est sophistiqué et le calcul dure 3 jours.
 |
| Calcul d’une instabilité de Kelvin-Helmholtz (R. Duvigneau, 2017). Cliquer pour animer. |
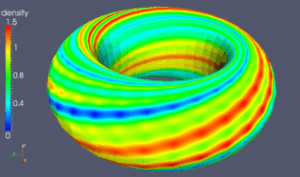
Notons également l’implication d’une vaste communauté interdisciplinaire (physiciens et mathématiciens) dans le grand projet international ITER pour mettre au point un équipement mettant en oeuvre une fusion nucléaire. Au niveau du calcul, il s’agit de résoudre des équations de magnéto-hydro-dynamique, qui combinent plusieurs domaines de la physique. Voici une illustration de cette activité et les moyens informatiques développés actuellement. En haut les travaux de M. Becoulet. En bas les travaux de M. Futanami.
 |
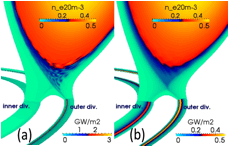 |
| Résolution des équations de magnéto-hydro-dynamique, dans le cadre du Projet ITER (B. Nkonga, 2016). Le flux magnétique, le courant, le tourbillon, le potentiel électrique, la vitesse parallèle, la densité, et la température sont prises en compte. Le plasma est en rotation dans le Tokamak (illustration du haut). Ce plasma est notamment contrôlé par un dispositif situé en bas de l’anneau (illustration du bas). |
Il est remarquable que la communauté aborde aujourd’hui des champs nouveaux en dehors des applications plus classiques à la physique ou à l’ingénierie. La modélisation mathématique et la simulation numérique du trafic routier ou piétonnier qui s’y rattache en offrent un exemple assez proche de la mécanique des fluides. Citons ici les travaux de P. Goatin. On illustre ci-dessous une simulation d’évacuation de salle par deux issues dont la première est rapidement congestionnée. L’objectif à terme de ce type de simulation est de mieux concevoir la salle afin d’une évacuation plus rapide en cas d’alerte.
 |
| Simulation de l’évacuation d’une salle en cas d’alerte. Cliquer pour animer (P.Goatin, 2013). Vue aérienne. Les personnes sont initialement massées à proximité du mur à gauche. Lorsque l’alerte est donnée, elles se dirigent vers l’issue la plus proche, qui, assez vite, se congestionne. Une partie du groupe se dirige alors vers l’issue de droite. |
Enfin, notons que les travaux initiés en 2000 sur la modélisation de la circulation sanguine cités précédemment ont pris de l’ampleur, comme en témoigne la figure ci-dessous qui illustre la montée en puissance du calcul (1 s de temps physique exige 500 000 pas de temps de simulation, soit 83 mn de temps calcul sur 24 cœurs du Mésocentre Régional Aquitaine, MCIA, en 2014), et la sophistication du modèle physico-numérique actuel (potentiel de membrane sur les ventricules, modèle géométrique du patient, hypothèses de structure des tissus; calcul: intégrateurs exponentiels pour la réaction).
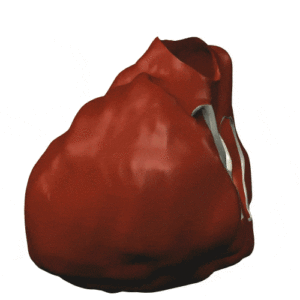 |
| Simulation de l’activité cardiaque dans le cadre du Projet CardioSense [4]. Cliquer pour animer. |
Après de tels succès, comment imaginez-vous les futurs progrès de votre discipline ?
Oui il y a eu des succès, grâce à beaucoup de travail et de trouvailles par les chercheur.e·s, et en même temps, on aurait bien aimé aller beaucoup plus vite !
Aujourd’hui nous avons conscience d’un certain nombre de défis vitaux pour l’humanité, dans les domaines de l’évolution de la planète (la préserverons nous ?), dans le domaine de la santé (les progrès de la médecine sont-ils pour tous ?), et de l’énergie (comment la décarboner ?). Les numéricien·ne·s ont un rôle important à jouer pour relever ces défis, mais cela implique de pouvoir transmettre leurs mathématiques et leurs algorithmes vers les sciences de la terre, la biologie, la médecine, etc.
On prévoit un plus grand impact de la modélisation de notre environnement et une exigence accrue en matière de sécurité des systèmes et d’environnement pour une régulation plus efficace des processus industriels et la conformité des produits à la réglementation, notamment en matière de contrôle de la pollution.
Aujourd’hui les plus gros calculs en termes de volumes d’opérations sont conduits par les grands industriels, souvent de l’industrie du transport ou de la défense. Le principe général est de décomposer le calcul global en blocs indépendants a priori plus simples à résoudre, de calculer chacun d’entre eux (éventuellement de façon parallèle), puis de fusionner l’ensemble. Les calculs moins volumineux mais complexes sont le plus souvent exécutés par des sociétés de service.
La sophistication de nos méthodes va s’accélérer, avec plus de mathématiques (précision, algorithmes de résolution, adaptation de maillage, identification, optimisation), la prise en compte de plus de lois physiques, couplant des phénomènes divers, la prise en compte des aléas.
Il faudra aussi que la programmation sur les futures architectures d’ordinateurs soit efficace, mais en proposant des outils pour lesquels les mécanismes trop complexes à guider (le maillage, le parallélisme, notamment) seront transparents pour l’ingénieur utilisateur ou des non-spécialistes: pourquoi-pas ne pas envisager des travaux de science participative impliquant des citoyen·ne·s ?
Jean-Antoine Désidéri & Alain Dervieux.
[1] M.O. Bristeau, 0. Pironneau, R. Glowinski, J. Périaux, P. Perrier, and G. Poirier: On the numerical solution of nonlinear problems in fluid dynamics by least squares and finite element methods (II). Application to transonic flow simulations, Computer Methods in Applied Mechanics and Engineering 51, 1985
[2] A. Dervieux, J.-A. Désidéri, F. Fezoui, B. Palmerio, J.P. Rosenblum, B. Stoufflet: Euler calculations by upwind Finite Element Methods and adaptive mesh algorithm, GAMM Workshop on the Numerical Simulation of Compressible Euler Flows, Rocquencourt (F), June 10-13 1986, Notes in Numerical Fluid Dynamics 26, Vieweg , Braunshweig-Wiesbaden
[3] M.V. Salvetti, M.C. Ciccoli and J.-A. Désidéri: Non-equilibrium external flows including wall-catalysis effects by adaptive upwind finite elements, Russian Physics Journal, 36:4, 1993
[4] S. Labarthe, J. Bayer, Y. Coudière, J. Henry, H. Cochet, P. Jaıs and E. Vigmond: A bilayer model of human atria: mathematical background, construction, and assessment, Europace 16:4, The Oxford University Press, 2014
Notes:
La notion de stabilité. Les solutions produites par simulation numérique résultent de la somme de deux composantes. La première, dite composante convergente, approche la solution exacte des équations aussi précisément que nécessaire par raffinement du maillage, quitte à augmenter le coût du calcul. La seconde est dite composante parasite. Lorsque le schéma d’approximation est « stable’’, la composante parasite reste à un niveau faible, intimement lié à la précision arithmétique des opérations élémentaires sur l’ordinateur. À l’inverse, si le schéma est instable, la composante parasite s’amplifie exponentiellement dans le déroulé de l’algorithme jusqu’à noyer complètement le résultat. Il est donc impérieux en analyse numérique d’établir de manière fiable les propriétés de stabilité des schémas d’approximation.