Un nouvel « Entretien autour de l’informatique ». Serge Abiteboul et Christine Froidevaux interviewent Claude Berrou, un informaticien et électronicien, membre de l’Académie des sciences. Claude Berrou est Professeur à IMT Atlantique. Il est notamment connu pour ses travaux sur les turbocodes, très utilisés en téléphonie mobile. Sa recherche porte aujourd’hui sur les neurosciences informationnelles.
Cet article est publié en collaboration avec TheConversation
English version
Binaire : Tu étais électronicien au départ, comment es-tu arrivé à l’informatique ?
CB : Je suis un randonneur des sciences. Après une formation initiale à l’école qui s’appelle aujourd’hui Phelma, j’ai fait un peu de tout : électronique, traitement de signal, architecture de circuits. Puis je suis arrivé à l’informatique… par hasard, avec les codes correcteurs et la théorie de l’information.
Binaire : Une question que nous adorons poser à Binaire, c’est quoi l’informatique pour toi ?
CB : J’ai un aphorisme : l’informatique est à la science, ce que le langage naturel est à l’intelligence. Avant l’informatique, la science, c’étaient des équations, des formules et des théorèmes. L’informatique a permis de mettre en place des séquences d’opérations, des processus, des procédures, pour pouvoir traiter des problèmes complexes. Du coup, c’est presque synonyme de langage et c’est très comparable au langage naturel qui oblige à structurer. De même qu’on a un langage commun, l’informatique propose des langages compréhensibles par tous.
Binaire : Tu as travaillé sur les codes correcteurs. Tu peux nous dire à quoi ça sert ?
CB : Quand on transmet de l’information, on veut récupérer le message émis parfaitement. Même si on a beaucoup d’utilisateurs, et une bande passante limitée. Si le message est binaire, à cause du bruit et des interférences qui perturbent la ligne, certains 0 émis vont devenir des 1 reçus, des 1 devenir des 0. Plus le bruit est important par rapport au signal, plus fréquentes sont de telles erreurs. Le rapport signal sur bruit peut être dégradé, par exemple, par de mauvaises conditions météo ou par des perturbations causées par d’autres communications qui s’exécutent en même temps. Avec autant d’erreurs, la qualité est déplorable. Pour éviter cela, on code l’information à l’émission en ajoutant de la redondance. Le défi, c’est d’être capable de récupérer relativement bien le message sans avoir à mettre trop de redondance, sans trop faire grossir le message. Nous avons un peu le même problème avec le stockage dans les mémoires de masse. Des bits peuvent permuter, peut-être à cause de l’usure du disque. On introduit aussi de la redondance dans ces systèmes pour pouvoir récupérer l’information.
Binaire : Tu nous parles de ta super invention, les turbocodes.
CB : Les turbocodes sont nés grâce au Titanic, lorsqu’il a fallu assurer la transmission sans câbles de vidéos pour visualiser cette épave (des travaux d’Alain Glavieux). Je me suis amusé à essayer de diminuer l’effet du bruit dans les transmissions, et j’ai pensé qu’on pourrait introduire dans le décodage, pour le traitement d’erreurs, le principe de contre-réaction, une notion classique en électronique.
Pour moi, l’interdisciplinarité est fondamentale ; l’innovation est souvent à l’interface des disciplines. Vous prenez une idée qui a prouvé qu’elle marchait quelque part dans les sciences, et vous essayez de l’adapter dans un tout autre contexte. L’idée à l’origine des turbocodes, c’est d’importer une technique d’électronique en informatique.
Quand on veut réaliser un amplificateur avec un gain élevé, on en met 2 ou 3 en série. Mais ça donne des trucs instables. Pour stabiliser le montage, on met en œuvre un principe de contre-réaction : renvoyer vers l’entrée de l’amplificateur une fraction de sa sortie, avec le signe « – » , cela atténue les variations intempestives.
Je suis parti d’un algorithme connu : l’algorithme de Viterbi. Il permet de corriger (s’il n’y a pas trop de bruit) les erreurs survenues lors d’une transmission à travers un canal bruité et peut donc être considéré comme un amplificateur de rapport signal sur bruit. Le décodeur de Viterbi connaît la loi algébrique qui a servi à construire la redondance du message codé et l’exploite dans un treillis (l’équivalent déterministe d’une chaîne de Markov) et délivre ainsi le message d’origine le plus probable. J’ai donc mis deux algorithmes de Viterbi en série. Et j’ai ensuite essayé d’implémenter la notion de contre-réaction dans le décodage. C’est délicat et je n’étais pas un expert du codage.
Un problème, c’est que l’algorithme de Viterbi fait des choix binaires : le bit a été permuté ou pas. Nous l’avons adapté, avec un collègue, Patrick Adde, pour qu’il fournisse des décisions probabilistes, ce qui améliore nettement la performance du décodeur qui suit.
Binaire : comment ça fonctionne ?
CB : Comme je l’ai expliqué, pour protéger un message, on ajoute de la redondance. Le turbocode réalise le codage sur deux dimensions. Une bonne analogie est une grille de mots croisés avec les dimensions verticale et horizontale. Si les définitions étaient parfaites, une seule dimension suffirait. On pourrait reconstruire la grille, par exemple, juste avec les définitions horizontales. Mais comme on ne sait pas toujours à quoi correspondent les définitions et qu’il peut y avoir des ambiguïtés (les analogues du bruit, des effacements de bits, etc.), on donne aussi les définitions verticales.
Le décodage ressemble un peu à ce que peut faire un cruciverbiste. Le décodeur travaille en ligne (il exploite les définitions horizontales), puis passe à la dimension verticale. Comme le cruciverbiste, le décodeur fait plusieurs passes pour reconstruire le message.
Avec tout ça, les turbocodes sont efficaces.
Binaire : On te croit. Des milliards d’objets utilisent cette technologie !
CB : Oui. Toutes les données médias sur la 3G et la 4G sont protégées par les turbocodes.
Binaire : Cela nous conduit à un autre Claude : Claude Shannon et la théorie de l’information ?
CB : Oui avec cet algorithme, on est en plein dans la théorie de l’information. J’ai d’ailleurs contribué récemment à l’organisation du colloque de célébration du centième anniversaire de la naissance de Shannon à l’IHP, un colloque passionnant.
Shannon a montré que toute transmission (ou stockage) idéale devait normalement se faire avec deux opérations fondamentales. D’abord, pour diminuer la taille du message, on le compresse pour lui enlever le maximum de redondance inutile. Ensuite, pour se protéger contre les erreurs, on lui ajoute de la redondance intelligente.
Shannon a démontré les limites des codes correcteurs en 1948 ! Les turbocodes atteignent la limite théorique de Shannon, à quelques dixièmes de décibels près !
Binaire : Et maintenant. Tu as glissé vers les neurosciences…
CB : Ma recherche actuelle porte sur les neurosciences informationnelles. Récemment, vous avez interviewé Olivier Faugeras qui vous a parlé des neurosciences computationnelles, une approche assez différente.
Mon point de départ, c’est encore l’information, cette fois dans le cerveau. Le cortex humain est assimilable à un graphe, avec des milliards de nœuds et des milliers de milliards d’arêtes. Il y a des modules spécifiques, et entre les modules, il y a des liens de communication. Je suis persuadé que l’information mentale, portée par le cortex, est binaire.
Les théories classiques font l’hypothèse que l’information est stockée par les poids synaptiques, des poids sur les arêtes du graphe. Je fais une autre hypothèse. Pour moi, il y a trop de bruit dans le cerveau ; c’est trop fragile, inconstant, instable ; l’information ne peut pas être portée par des poids mais par des assemblées de nœuds. Ces nœuds forment une clique au sens géométrique du terme, c’est-à-dire qu’ils sont tous reliés deux à deux. Cela devient une information numérique.
Binaire : C’est là que nous allons retrouver le codage et la redondance ? Pour éviter que l’information ne se perde dans le cerveau, il y a aussi des redondances ?
CB : Oui. Pour l’école classique c’est-à-dire analogique, l’information est portée par les synapses. En ce cas, la redondance ne pourrait être assurée que par des répétitions : plusieurs arêtes porteraient la même information.
Selon notre approche, l’information est codée dans les connexions d’une assemblée de nœuds. La redondance est présente de façon naturelle dans ce type de codage. Prenez une clique de 10 nœuds dans un graphe. Vous avez 45 connexions dans la clique. Le nombre de connexions est grand par rapport au nombre de nœuds. Je m’appuie sur la règle de Hebb (1949) : lorsqu’un neurone A envoie des spikes et qu’un neurone B s’active systématiquement, la liaison entre A et B va se renforcer si elle existe, et si elle n’existe pas elle va être créée. La clique étant redondante, cela va résonner, une liaison altérée va se renforcer : grâce à la règle de Hebb on a une reconstruction en cas de dégradation. Nous avons bâti toute une théorie autour de ça.
Binaire : tu nous as largué. Pour faire simple, une clique porte un morceau d’information. Et le fait qu’il y ait tant de redondance dans la clique garantit la pérennité de l’information ?
CB : Oui. Et en plus, la clique peut être l’élément de base d’une mémoire associative. Je vais pouvoir retrouver l’information complète à partir de certaines valeurs du contenu. Et ça, c’est dû à la structure fortement redondante des cliques.
Binaire : Votre travail consiste en quoi ?
CB : J’ai mis en place une équipe pluridisciplinaire composée de neuropsychologues, neurolinguistes, informaticiens, etc. Nous essayons de concevoir un démonstrateur, une machine inspirée par le modèle du cerveau que nous imaginons, à l’échelle informationnelle. Dans un ordinateur classique, la mémoire est d’un côté et le processeur de l’autre. Dans notre machine, comme dans le cerveau, tout est imbriqué.
Selon la théorie que nous développons (pas encore complètement publiée), l’information mentale s’appuie sur des petits bouts de connaissance qui sont stockés dans des cliques. Les cliques sont choisies au hasard. Mais quand c’est fait, elles sont définitives. D’un individu à un autre, ce ne sont pas les mêmes cliques qui portent la même information. J’aimerais arriver à faire émerger de l’intelligence artificielle avec ce modèle de machine.
Binaire : Quelle est ta vision de l’intelligence artificielle ?
CB : Il y a en fait deux intelligences artificielles. Il y a d’abord celle qui s’intéresse aux sens, à la vision, à la reconnaissance de la parole par exemple. On commence à savoir faire cela avec le deep learning. Et puis, il y a celle qui nous permet d’imaginer et de créer, de savoir répondre à des questions inédites. Ça, on ne sait pas faire pour le moment. Pour moi, la seule façon d’avancer sur cette IA forte est de s’inspirer du cortex humain.
Ce sujet me passionne. J’aimerais le voir progresser et continuer à faire longtemps de la recherche.
Entretien recueilli par Serge Abiteboul et Christine Froidevaux
Voir aussi dans Binaire, Shannon, information et Sudoku
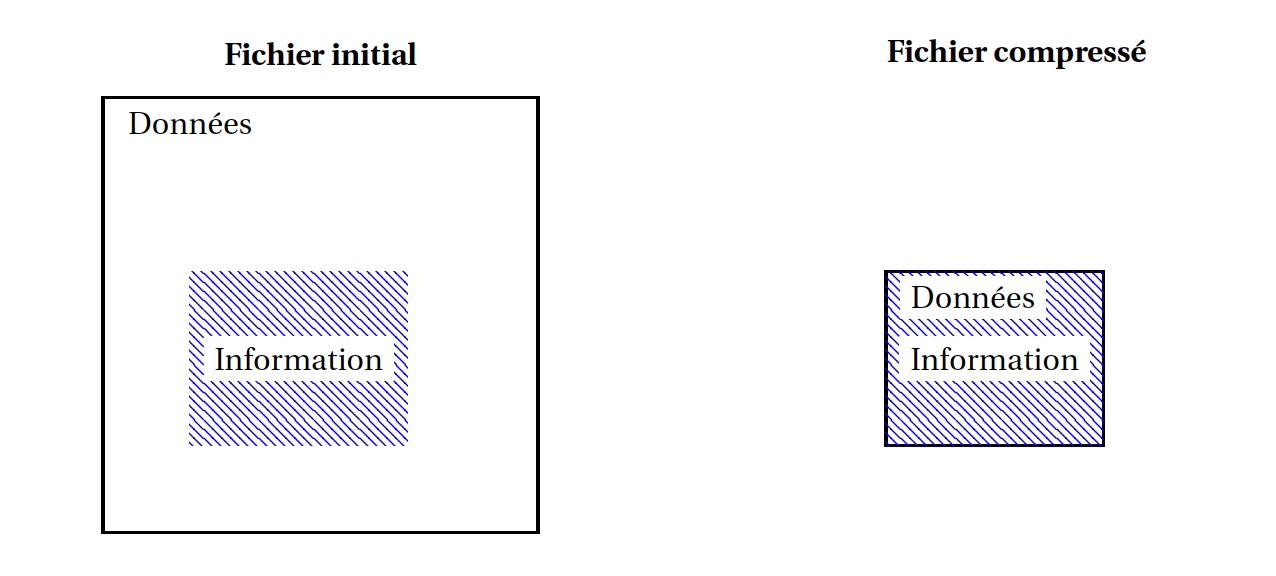La redondance
NetPublic est un site édité par l’
