De l’apprentissage à l’éducabilité, de Vapnik à Valiant

Pour mieux situer les travaux de Leslie Valiant, il faut évoquer ceux conduits antérieurement en URSS par Vladimir Vapnikⁱ.

La dimension de Vapnik-Chervonenkis (VC-dimension). 

La motivation de Vapnik et ses collègues est purement statistique : comment assurer qu’un modèle minimise à la fois l’erreur sur les données d’apprentissage (erreur empirique) et l’erreur de généralisation sur l’ensemble des données ? Comme lors des sondages électoraux, par exemple : s’assurer que ce qui est approximativement vrai sur un échantillon, l’est toujours à peu près sur toute la population visée.

Cette propriété, appelée convergence uniforme, n’est évidemment pas satisfaite en général. En fait, si un modèle possède tellement de paramètres à ajuster, qu’il puisse coller très précisément et de manière spécifique aux données d’apprentissage, il ne saura pas bien prédire des données plus générales.

La VC-dimension est un indicateur de ces classes de modèles – souvent désignées par le terme de classes de concepts – qui conditionne la convergence uniforme. 

Pour définir la VC-dimension, considérons un ensemble de données et une classe de modèles. Pour chaque modèle, une donnée satisfait ou ne satisfait pas ce modèle. Par exemple, si l’on considère comme données les points d’un carré de taille 1 du plan, et comme modèles les portions de demi-plans inférieuresⁱⁱ, alors pour tout demi-plan, une donnée appartient ou non à ce demi-plan.
La suite de la définition repose sur la possibilité pour les modèles de prédire si les données correspondent ou pas au modèle. On parle de pulvériser (shatter) des échantillons finis de données pour une classe C de modèles et un échantillon D de données, si pour tout sous-échantillon D’ de D, il existe un modèle de C tel que D’ est la partie de D satisfaisant ce modèle.

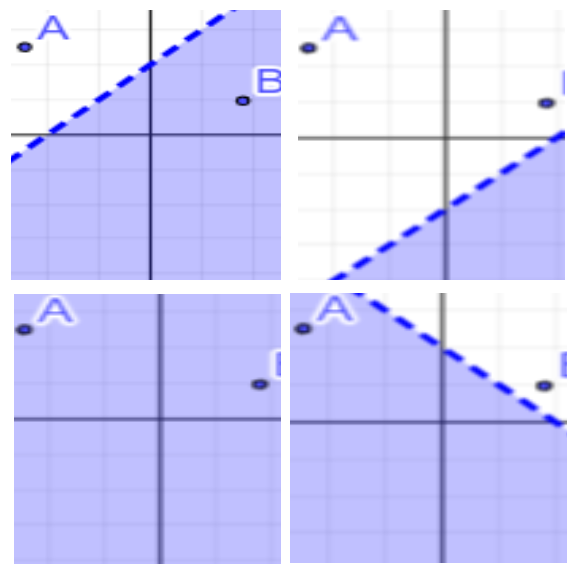
La Figure 1 illustre que tout couple de points peut être pulvérisé par des demi-plansⁱⁱⁱ. Par contre un échantillon de 3 points n’est pas pulvérisé^iv. La VC-dimension d’une classe de modèles C est alors le plus grand nombre d’échantillons d tel que tous les échantillons D de cette taille soient pulvérisables.

Dans notre exemple, la classe des fonctions affines (ces droites qui définissent des demi-plan) est donc de VC-dimension 2, puisqu’elles pulvérisent tous les couples de 2 points, mais pas de 3.

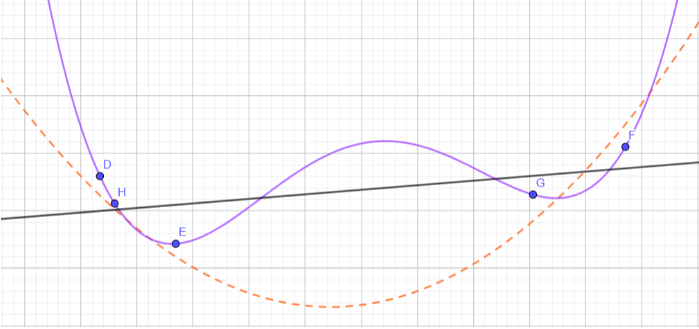
La Figure 2 illustre l’influence de la VC-dimension. Une parabole (que l’on ignore) définit la fonction à approximer à partir d’échantillons bruités. La classe des fonctions affines (VC-dimension 2) est trop pauvre, l’erreur empirique est grande. La classe des polynômes de degré 5 (VC-dimension 6) est trop riche, elle permet un sur-apprentissage (erreur empirique faible ou nulle mais erreur de généralisation forte).

Dans leur papier fondateur, Vapnik et Chervonenkis établissent que la convergence est uniforme si et seulement si la VC-dimension est finie, et ils bornent en fonction de cette dimension la taille des échantillons nécessaires pour obtenir un résultat d’une précision donnée.

 Du cadre de pensée de Vapnik à l’ingénierie algorithmique de Valiant

En un mot : un algorithme ne rase pas gratis^vi . Les travaux de Vapnik et Chervonenkis sur la VC-dimension sont publiés en anglais en 1971 dans une revue soviétique renommée. Lorsqu’il introduit l’apprentissage PAC treize ans plus tard, Valiant ne cite pas Vapnik. Pourtant dans la foulée du papier de Valiant il est vite démontré  qu’un concept est PAC apprenable si et seulement si sa VC-dimension est finie.

Il y a donc une concordance entre l’approche statistique et l’approche algorithmique,  résultat remarquable qui ancre la problématique de l’apprentissage^vii. Et c’est la notion de complexité algorithmique promue par Valiant qui a depuis inspiré l’essentiel des recherches en informatique, parce qu’en général la VC-dimension ne dit pas grand-chose du fait qu’il puisse exister un algorithmique d’apprentissage.

 L’ingénierie algorithmique de Valiant appliquée au réseaux de neurones

 On peut voir également les réseaux d’apprentissage profond avec des neurones artificiels comme des classes de concepts. Une architecture constitue une classe dans laquelle l’apprentissage consiste à trouver un concept en ajustant les coefficients synaptiques. Il est difficile d’en estimer la VC-dimension mais celle-ci est considérable et n’aide pas à expliquer l’efficacité. Comme l’évoquait Yann le Cun déjà cité, l’efficacité d’un réseau profond de neurones et l’importance de bien le dimensionner sont à rechercher dans son adéquation aux structures cachées du monde où il apprend, ce qui rejoint à très grande échelle la problématique sommairement illustrée par la Figure 1. On perçoit bien que disposer d’un cadre théorique solide, ici la notion d’apprenabilité, fournit un cadre de pensée mais ne fournit pas l’ingénierie nécessaire pour le traitement d’une question particulière. Les recherches ont de beaux jours devant elles. Pour en savoir beaucoup plus sur l’apprentissage en sciences informatiques et statistiques, les cours, articles et ouvrages accessibles sur le net ne manquent pas. Le panorama précis de Shai Shalev-Shwartz et Shai Ben-David^viii peut être combiné avec les vidéos des cours de Stéphane Mallat, titulaire de la chaire de sciences des données au Collège de France.

Max Dauchet, Université de Lille.

i Vapnik, V. N., & Chervonenkis, A. Y. (1971). « On the Uniform Convergence of Relative Frequencies of Events to Their Probabilities. » Theory of Probability and its Applications, 16(2), 264-280.

ii Ensemble des points sous la droite frontière. Il faut en effet considérer les demi-plans et non les droites pour appliquer rigoureusement la définition en termes d’appartenance d’une donnée à un concept.

iii Sauf si les deux points ont même abscisse, ce qui a une probabilité nulle. Pour un échantillon de deux données, il y a 4 cas à étudier, et il y en a 2^dpourddonnées.

iv A delà des fonctions affines, qui sont des poylynômes de degré 1, on établit sans peine que la classe des polynômes de degré n est de VC-dimension n+1. La classe de l’ensemble des polynômes est donc de VC-dimension infinie.

v Soit A le point de plus faible ordonnée. Pour aucun demi-plan inférieur A n’est au dessus et les deux autres points en dessous de la droite frontière.

vi En référence au No-Free-Lunch -Theorem qui stipule qu’il n’y a pas d’algorithme universel d’apprentissage.

vii Valiant passera toujours les travaux de Vapnik sous silence, on peut se demander pourquoi, alors qu’il aurait pu faire de la VC-dimension un argument en faveur de la pertinence de sa propre démarche sans prendre ombrage de Vapnik. C’est qu’en général la VC-dimension ne dit pas grand-chose de la praticabilité algorithmique. En effet, pour de nombreuses classes C d’intérêt, le nombre n de paramètres définit une sous classe Cn : c’est le cas pour le degré n des polynômes, la dimension n d’un espace ou le nombre n de variables d’une expression booléenne. Or, c’est la complexité relative à cet n qu’adresse l’algorithmique et la VC-dimension de Cn ne permet pas de la calculer, même si elle est parfois de l’ordre de n comme c’est le cas pour les polynômes. Ainsi, selon les concepts considérés sur les expressions booléennes à n variables ( les structures syntaxiques comme CNF, 3-CNF, DNF ou 3-terms DNF sont des classes de concepts), il existe ou il n’existe pas d’algorithme d’apprentissage en temps polynomial relativement à n, même si la VC-dimension est polynomiale en n.

viii Shai Shalev-Shwartz and Shai Ben-David, Understanding Machine Learning :From Theory to Algorithms, Cambridge University Press, 2014.